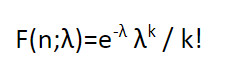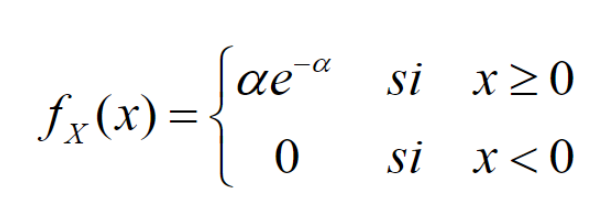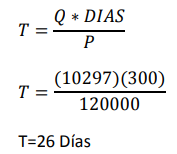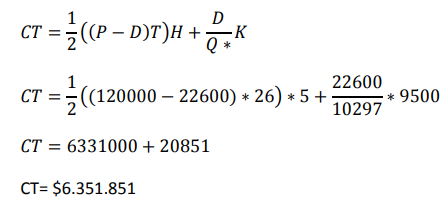1. Relación de conceptos
Tipos comunes de aplicaciones:
a. Diseño operación de sistemas de colas
- Sistema de colas con un sólo servidores.
- Sistema de colas con dos servidores.
- Sistemas de colas múltiples en serie.
- Sistemas de colas múltiples en paralelo.
b. Administración de sistemas de inventario:
- Modelo de inventario de cantidad económica de pedidos.
- Modelo de inventario de cantidad de producción.
- Aleatorio el Modelo de inventario con demandas probabilística.
Otros tipos de aplicaciones de simulación
- Generación de observaciones aleatorias a partir de una distribución de probabilidad.
- Proceso de simulación aplicadas a los modelos econométricos en la análisis de la demanda y de la oferta.
2. Diseño y operación de sistemas de colas
La teoría de colas es una formulación matemática para la optimización de sistemas en que interactúan dos procesos normalmente aleatorios: un proceso de llegadas de clientes y un proceso de servicio a los clientes, en los que existen fenómenos de acumulación de clientes en espera del servicio y donde existen reglas definidas (conductos) para la prestación del servicio.
Sistemas de colas con un solo servidor
Es un proceso markoviano, es decir un proceso en cadena de variables aleatorias, en el cual se tiene un solo servidor. El tiempo de llegada se desprende de la distribución de Poisson, mientras el tiempo de atención o de servicio al cliente se desprende de una distribución exponencial. A continuación una explicación de la distribución de Poisson y la distribución exponencial:
1. Distribución Poisson
Es la probabilidad de un número n de eventos ocurriendo en un tiempo fijo si estos eventos ocurren con una tasa media conocida, y son independientes del tiempo desde el último evento.
Ejemplo
El número medio de pacientes admitidos por día en la sala de emergencias de un hospital pequeño es 2. Si solo hay cuatro camas disponibles en dicha sala ¿Cuál es la probabilidad de que un día cualquiera el hospital no tenga camas suficientes para acomodar los pacientes que lleguen?
P(x = 0) = e-220/0!= 0,13 * 100 = 13%
La probabilidad de que un día cualquiera el hospital no tenga camas suficientes para acomodar los pacientes que lleguen es del 13%.
2. Distribución Exponencial
Se dice que una variable aleatoria continua X que toma todos los valores no negativos tiene una distribución exponencial con parámetro de escala:
si la función de densidad de probabilidad es:
La ecuación de la distribución exponencial es:
Ejemplo
El número de automóviles que corren en una vía de Bogotá a alta velocidad durante un lapso de una hora en cierta autopista es con ?=1. ¿Cuál es la probabilidad de tener un tiempo de espera menor de 2 minutos entre automovilistas sucesivos que circulan a alta velocidad?
F(X,? )= 1e-1(2) = 1e-2 = 0,14*100 =14%
La probabilidad de tener un tiempo de espera menor de 2 minutos entre automovilistas sucesivos que circulan a alta velocidad es del 14%.
Parámetros del modelo de teoría de colas de un solo servidor
| El número promedio de unidades en el sistema | L= ?/ (? -?) |
| El número promedio de unidades que esperan ser atendidas en la cola | Lq = ?2/ ? (? -?) |
| El tiempo promedio de una unidad en el sistema | W= 1 / (? -?) |
| El tiempo promedio de una unidad en la cola | Wq= ?/ ? (? – ?) |
Sistemas de colas con dos servidores
Este modelo supone llegadas y tiempos de servicio aleatorios para canales de servicio múltiples, teniendo en cuenta las mismas consideraciones que en el modelo anterior, excepto que ahora existe una sola fila de entrega que alimenta a los canales de múltiples de servicio con igual tasa de servicio.
Parámetros del modelo de teoría de colas de un solo servidor
| La probabilidad de que el sistema este vacío | Po = 1 / ( ?1/n! (?/?)n + 1/s! ( ?/?)s(s?/s?-?)) |
| La probabilidad de que el sistema esté ocupado | P(sistema esté ocupado)= (PS (?S) / S! (?S / ?S -?)) * P0 |
| El número promedio de unidades en el sistema | L= P(sistema esté ocupado)* p?/ (s – p?) + p |
| El número promedio de unidades que esperan ser atendidas en la cola | Lq= P(sistema esté ocupado)* p?/ (s – p?) |
| El tiempo promedio de una unidad en el sistema | W= 1/?(P(sistema esté ocupado)* p?/ (s – p?) + p) |
| El tiempo promedio de una unidad en la cola | Wq= 1/?(P(sistema esté ocupado)* p?/ (s – p?) ) |
Sistema colas servidores múltiples en serie
Este tipo de líneas de espera es característico del sector productivo, donde las líneas de ensamble requieren de una serie de actividades que se desarrollan en serie.
Sistema colas con servidores múltiples en paralelo
Consiste en el cambio de la estructura que aseguren la atención al cliente por el orden de llegada, se debe de tener una sola cola, que al quedar libre un servidor se le asigna al cliente que continua.
Ejemplo:
- Ventanillas de los bancos
- Cajas de los supermercados
- Una panadería o una peluquería
3. Administración de sistemas de inventario
Los inventarios son aquellos materiales o bienes ociosos que la organización conserva para su uso en algún momento en el futuro.
Características de los modelos de inventario
Las siguientes son las características que componen sus elementos:
- Demanda Independiente: dos o más artículos en los que la demanda de un artículo no afecta la demanda de cualquiera de los otros artículos.
- Demanda dependiente: dos o más artículos en los que la demanda de un artículo determina o afecta la demanda de uno o más de los otros artículos.
- Demanda determinística: la demanda del artículo por periodo se conoce con certeza.
- Demanda probabilística: la demanda del artículo por periodo está sujeta a una cantidad que cambia con el tiempo y es variable.
- Déficit: es una circunstancia en la que el inventario no dispone de la suficiente cantidad de artículos para satisfacer la demanda.
- Tiempo Líder: el tiempo entre colocación de un pedido de productos y la llega de estos enviados por el proveedor.
- Descuento: este depende de la cantidad del lote del pedido y el precio a pagar por el consumidor.
Nomenclatura
| El costo del pedido u organización (K) | Es el costo fijo por colocar un pedido para reabastecer el inventario. |
| El costo de compra (C ) | Es el costo por unidad del producto para la compra. |
| El costo de conservación (H) | El costo del producto por permanecer en inventario. |
| Tasa de transferencia (I) | La fracción del costo de compra del artículo para determinar la variación en el incremento o modificación del costo de conservación. |
| Costo de déficit (B) | Costo asociado a la no satisfacción de la demanda del producto. |
Modelo de inventario de cantidad económica de pedidos (EOQ)
Es la cantidad de económica de pedido que busca disminuir el costo del inventario de la organización.

Ejemplo:
Una empresa de Medellín de confección surte almacenes éxito con tres sus productos tradicionales, la cual realizó un estudio de mercadeo para disminuir el costo. La demanda de artículos de artículos para tres ciudades es de120 unidades mensuales para Medellín, para Bogotá de 150 unidades y Cali de 130 unidades mensuales. El costo de preparación de la orden es de $1000 para Bogotá, a Cali de $500 y a Medellín de $400 por orden y el costo que le representa el almacenamiento por unidad en el mes es de $100, Utilizando los datos, se pide plantear un modelo EOQ y se pide determinar sus parámetros. La empresa trabaja 360 días al año. Además cual produce los costos mínimos y los costos más altos.
Solución:
Información
| Bogotá | Cali | Medellín | |
| Demanda | 150 | 130 | 120 |
| Costos de orden (S) | 1000 | 500 | 400 |
| Costo de almacenamiento (H) | 100 | 100 | 100 |
Cantidad optima de pedidos:
| Bogotá | Cali | Medellín | |
| Demanda | 150 | 130 | 120 |
| Costos de orden (S) | 1000 | 500 | 400 |
| Costo de almacenamiento (H) | 100 | 100 | 100 |
| Cantidad optima de pedidos | 55 | 36 | 31 |
- La cantidad óptima de pedidos para Bogotá es de 55 artículos.
- La cantidad óptima de pedidos para Cali es de 36 artículos.
- La cantidad óptima de pedidos para Medellín es de 31 artículos.
Número esperado de órdenes
N=D/Q
| Bogotá | Cali | Medellín | |
| Demanda | 150 | 130 | 120 |
| Cantidad optima de pedidos | 55 | 36 | 31 |
| Número de ordenes | 3 | 4 | 4 |
- El número de órdenes de pedido es para Bogotá de 3.
- El número de órdenes de pedido es para Cali de 4.
- El número de órdenes de pedido es para Medellín de 4.
Tiempo esperado entre órdenes
| Bogotá | Cali | Medellín | |
| Días | 360 | 360 | 360 |
| Número de ordenes | 3 | 4 | 4 |
| Tiempo esperado entre órdenes | 120 | 90 | 90 |
- El tiempo esperado entre órdenes para Bogotá es de 120 días al año.
- El tiempo esperado entre órdenes para Cali es de 90 días al año.
- El tiempo esperado entre órdenes para Medellín es de 90 días al año.
El costo total
| Costo total | Bogotá | Cali | Medellín |
| Demanda | 150 | 130 | 120 |
| Costo de ordenes (s) | 1000 | 500 | 400 |
| Costo de almacenamiento (H) | 100 | 100 | 100 |
| Cantidad optima de pedidos | 55 | 36 | 31 |
| Costo total | 5477 | 3606 | 3098 |
- El costo total de pedidos para Bogotá es de $5477
- El costo total de pedidos para Cali es de $3606
- El costo total de pedidos para Medellín es de $3098
EL que le representa el costo más alto es Bogotá con $5477 y el mínimo costo Medellín con $3098.
Modelo de inventario de cantidad de producción
El modelo de inventario presentado es similar al primer modelo por el hecho de que esté intentando determinar cuánto debemos pedir y cuando hacerlo. Este modelo está diseñado para situaciones de producción en las que una vez colocado el pedido se inicia la producción y diariamente se va agregando el inventario de un número constante de unidades, hasta que se vaya complementado el lote de producción.
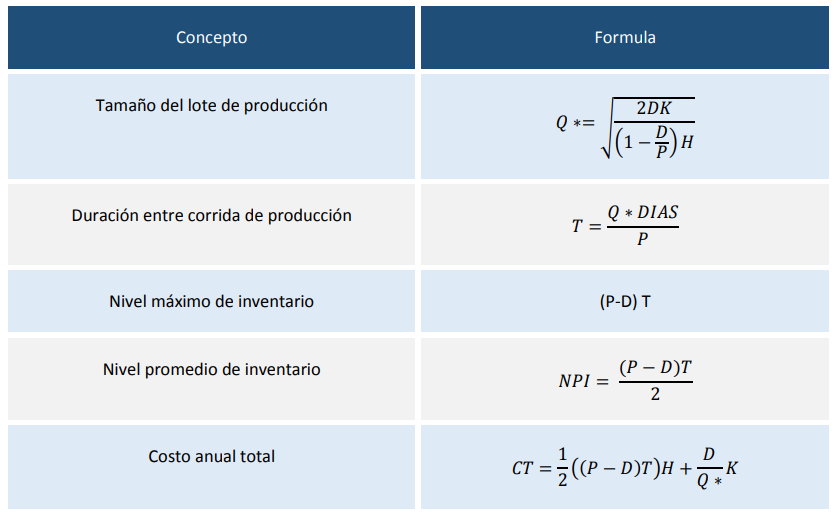
Ejemplo:
Una empresa de manzanas, produce una línea de producción con capacidad anual de 120.000 cajas de sus productos tradicionales. La demanda anual se estima en 22600 cajas, manteniendo la tasa de demanda constante en el año. El costo de la organización para la entrega del producto cuesta $9500. El costo de manufactura y el costo anual de posesión es de $5. Utilizando estos datos determinar las diferentes medidas del modelo sabiendo que trabaja 300 días al año.
Solución:
- ¿Cuál es el tamaño de lote de producción?
Q* = $10.297
2. Duración entre corrida de producción?
3. ¿Nivel máximo de Inventario?
(P-D)T = (120000 – 22600)(26) = 2.532.400
4. Nivel Promedio de inventario?
5. ¿Costo anual total?
Modelo de inventario con demanda pirobalística
Se supone que se conoce la distribución de probabilidad para la demanda, pero que esa demanda es impredecible en un día o mes dado. La incertidumbre al predecir la demanda significa que siempre existe la probabilidad de que haya faltantes, es decir, de quedar sin artículos en la entidad. El riesgo puede reducirse teniendo un inventario grande, pero nunca puede eliminarse. La tarea es balancear el riesgo ocasionado por los faltantes y del costo que se tiene por la existencia adicional.