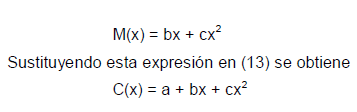Los economistas y las personas relacionadas con los negocios se interesan en la manera en que variables como el inventario, la producción, la oferta, la publicidad y el precio afectan a otras variables como las utilidades, los ingresos, la demanda, la inflación y el empleo.
Tales problemas se estudian usando análisis marginal. El término marginal es empleado por los economistas para una razón de cambio o derivada.
Tres funciones de importancia para un economista o un fabricante son:
C(x) = Costo total de producción de x unidades de un producto durante algún período.
R(x) = ingresos totales recibidos de la venta de x unidades del producto durante el período.
P(x) = utilidades totales obtenidas al vender x unidades del producto durante el período.
Estas se denominan, respectivamente:
– Función de costo,
– Función de ingreso y
– Función de utilidad.
Si se venden todas las unidades producidas, entonces estas funciones se relacionan por
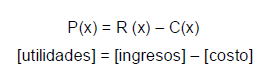
Las derivadas C´(x), R´(x) y P´(x) se denominan el costo marginal, los ingresos marginales y las utilidades marginales, respectivamente.
Si se venden todas las unidades producidas, entonces una relación entre ellas se obtiene al derivar:
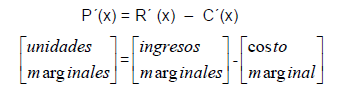
Las cantidades P´(x), R´(x) y C´(x) representan las razones instantáneas de cambio de las utilidades, los ingresos y el costo con respecto a x, donde x es la cantidad del producto producido y vendido.
En la práctica, con frecuencia C´(x) se interpreta como el costo de fabricación de la (x+1)ava unidad. Si bien esto no es exacto, por lo general es una buena aproximación, puesto que
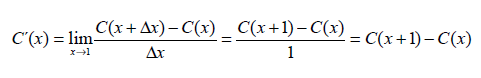
Esta aproximación es razonable puesto que x por lo general es grande y x =1 puede considerarse próxima a cero por comparación. Puesto que C(x+1) es el costo de producción de x+1 unidades y C(x) es el costo de producción de x unidades, se sigue que C´(x)? C(x+1) – C(x) es el costo de producción aproximado de la (x+1) ava unidad. De una manera similar, R´(x) son los ingresos aproximados recibidos de la venta de la (x+1) ava unidad.
El costo total de producción, C(x), de x unidades puede expresarse como un asuma C(x) = a + M(x)bdonde a es una constante , llamada gastos generales fijos, y M(x) es una función que representa el costo de fabricación.
Los gastos generales que incluyen costos fijos, como rentas y seguros, no dependen de x; deben pagarse aún cuando no se produzca nada.
Por otra parte, el costo de fabricación, M(x), que incluye aspectos como el costo de materiales y mano de obra, depende del número de artículos fabricados. En economía se señala que con las suposiciones de simplificación adecuada M(x) puede expresarse en la forma
Fuente: Apuntes de matemáticas de UNIDEG