Muchos problemas importantes en ingeniería y contabilidad dependen de la determinación de la recta tangente a la gráfica de una función en un punto específico. Esta sección inicia con la definición de lo que significa recta tangente y como se calcula la ecuación de la misma.
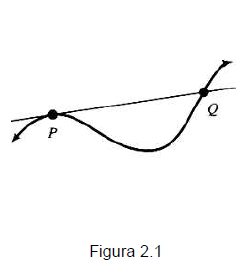
Como recordarás de tus cursos de geometría básica, la recta tangente en un punto de una circunferencia se definió como la recta que intersecta a la circunferencia en un sólo punto. Para una curva en general la tangente en un punto puede no ser tangente en otros puntos, es el caso de la curva de la figura 2.1. La recta tangente en el punto P no es tangente en el punto Q.
Para obtener una definición adecuada de la recta tangente a la gráfica de una función en un punto, se empleará el concepto de límite a fin de definir la pendiente de la recta tangente en un punto.
Después, la recta tangente se determinará por medio de su pendiente y el punto de tangencia.
Considera una función f continua en un punto x1 de su dominio. Traza una recta que pase por los puntos P de coordenadas (x1, f (x1 )) y Q de coordenadas (x2 , f (x2 )) como lo muestra la figura 2.2 . Cualquier recta que pase por dos puntos P y Q como se describen aquí se denomina recta secante.
Si observas detenidamente la figura te darás cuenta de que la pendiente de la recta secante está dada por la expresión
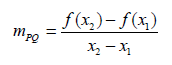Nota: Si no recuerdas como se calcula la pendiente revisa tu antología de matemáticas básicas.
La diferencia de las abscisas (las coordenadas x) de P y Q se denotará por ?x (se lee “delta x”) de forma que 
y como
la expresión para la pendiente puede escribirse como
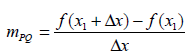
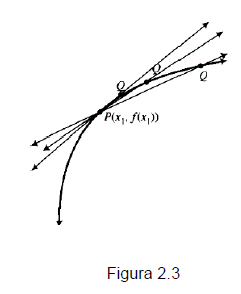
Ahora, considera el punto P como un punto fijo y que el punto Q se mueve a lo largo de la curva hacia P. Esto equivale a decir que ?x tiende a cero.
Conforme esto sucede, la recta secante gira sobre el punto fijo P (ver figura 2.3); a medida que el punto Q se acerca al punto P ?x ? 0 y la recta secante se convierte en una recta tangente a la curva en el punto (x1, f (x1 )) . Con punto P (x1, f (x1 )) , de la siguiente manera:
Definición: Suponga que la función f es continua en x1 . La recta tangente a la gráfica de f en el punto P (x1, f (x1 )) tiene pendiente m(x1 ) dada por
La pendiente de la recta tangente a la gráfica de una función se denomina pendiente de la gráfica en el punto.
Fuente: Apuntes de matemáticas de UNIDEG