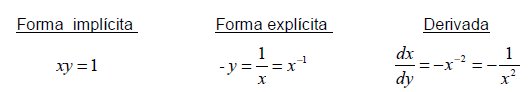Funciones explicitas e implícitas
Hasta aquí la mayor parte de las funciones aparecidas en el texto estaban expresada en forma explícita, como por ejemplo la ecuación:
donde la variable y está escrita explícitamente como función de x . Algunas funciones, por el contrario, están implícitas en la ecuación. Así, la función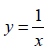 
viene definida x implícitamente por la ecuación 
.
Supongamos que se nos pide hallar la derivada dx para esta ecuación. Podemos dy empezar escribiendo y como función explícita de x, derivando a continuación.
Esta estrategia funciona siempre que seamos capaces de despejar y en la ecuación. Pero si no se logra despejar y, no es factible este método. Por ejemplo, ¿cómo hallar
donde resulta muy difícil despejar y como función de x?. En tales situaciones se debe usar la llamada derivación implícita .
Para comprender la técnica de la derivación implícita es preciso tener en cuenta que la derivación se efectúa con respecto de x, esto quiere decir que cuando debamos derivar términos que solo contienen a x la derivación será la habitual.
Sin embargo cuando tengamos que derivar un término donde aparezca la variable y, será necesario aplicar la regla de al cadena ya que se está suponiendo que y viene definida implícitamente como función de x.
Estrategias para la derivación implícita
1. Derivar ambos lados de la ecuación respecto de x.
2. Agrupar todos los términos en que aparezca dy/dx en el lado izquierdo de la ecuación y pasar todos los demás a la derecha.
3. Sacar factor común en el miembro de la izquierda .
4. Despejar dy/dx.
Fuente: Apuntes de matemáticas de UNIDEG