Por 
denotamos el hecho de que f (x) tiende a “A” cuando x
tiende hacia “ a ” por valores menores que “ a ” , es decir, cuando x tiende hacia “ a ”
por la izquierda . Análogamente, 
significa que x tiende hacia “ a ”
por valores mayores que “ a ”, o sea, cuando x tiende hacia “ a ” por la derecha .
Cuando decimos que 
existe significa que los límites por la izquierda y por la derecha son iguales, esto es
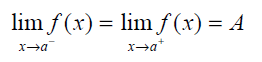
Nota: La existencia del límite por la izquierda no implica la existencia del límite por la derecha, y recíprocamente.
Cuando la función está definida sólo a un lado del punto “ a ” , entonces 
es lo mismo que el límite lateral, si existe. Por ejemplo, la figura 1.15 muestra la gráfica de la función
. Observa como ésta función está definida sólo a la derecha de cero, por lo tanto
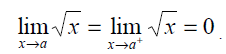
Naturalmente el límite por la izquierda no existe, pues x no está definida para x < 0.
Fuente: Apuntes de matemáticas de UNIDEG